La regla de Cramer se aplica para resolver sistemas de ecuaciones lineales que cumplan las siguientes condiciones:
1 El número de ecuaciones es igual al número de incógnitas.
2 El determinante de la matriz de los coeficientes es distinto de cero.
Ejemplo:
Ejemplo de la resolución de un sistema simple de 2x2:
Dado
que matricialmente es:
x e y pueden ser resueltos usando la regla de Cramer

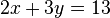
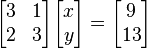
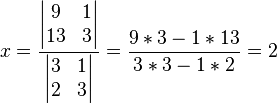
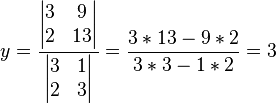
No hay comentarios:
Publicar un comentario