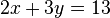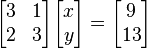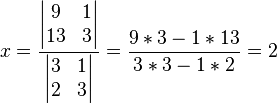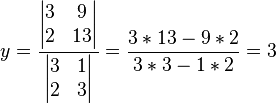Como Hallar La Hipotenusa!

Los pasos a seguir serán los siguientes:

	Cuando se calcula la hipotenusa aplicamos directamente el Teorema de Pitágoras
	Sustituimos cada cateto por su valor: el cateto x por 4 , el cateto y por 3
	Realizamos los cuadrados
	Sumamos
	Como la hipotenusa está elevada al cuadrado, hay que hacer la raíz
	Solución final: la hipotenusa vale 5

A CONTINUACION UN VIDEO EXPLICATIVO:

Teorema Del Cateto

En todo triángulo rectángulo un cateto es media proporcional entre la hipotenusa y su proyección sobre ella.

a  hipotenusa

b y c  catetos

m  proyección del cateto b sobre la hipotenusa

n  proyección del cateto c sobre la hipotenusa

EJEMPLO:

La hipotenusa de un triángulo rectángulo mide 30 cm y la proyección de un cateto sobre ella 10.8 cm. Hallar el otro cateto.

A CONTINUACION UN VIDEO EXPLICATIVO:

Teorema De Pitagoras!

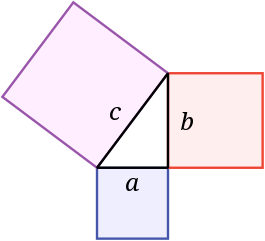El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de los cuadrados de los catetos (los dos lados menores del triángulo, los que conforman el ángulo recto).

A CONTINUACION UN VIDEO EXPLICATIVO:

Regla de Sarrus

La regla de Sarrus es un método fácil para memorizar y calcular un determinante 3×3. Recibe su nombre del matemático francés Pierre Frédéric Sarrus.
                                               

Pierre Sarrus (1798, 1861) fue un matemático francés que estableció una regla para calcular determinantes de orden 3.
Los términos con signo + están formados por los elementos de la diagonal principal y los de las diagonales paralelas con su correspondiente vértice opuesto.

Regla De Cramer!

La regla de Cramer se aplica para resolver sistemas de ecuaciones lineales que cumplan las siguientes condiciones:

 1  El número de ecuaciones es igual al número de incógnitas.

 2  El determinante de la matriz de los coeficientes es distinto de cero.

Ejemplo:

Ejemplo de la resolución de un sistema simple de 2x2:

Dado

que matricialmente es:

x e y pueden ser resueltos usando la regla de Cramer

Metodo De Reduccion!

AQUI ESTAN LOS PASOS PARA RESOLVER POR METODO DE REDUCCION:

1. Se preparan las dos ecuaciones, multiplicándolas por los números que convenga.

2. La restamos, y desaparece una de las incógnitas.

3. Se resuelve la ecuación resultante.

4. El valor obtenido se sustituye en una de las ecuaciones iniciales y se resuelve.

5. Los dos valores obtenidos constituyen la solución del sistema.

Y A CONTINUACION UN VIDEO:

Metodo De Sustitucion!

AQUI ESTAN LOS PASOS PARA RESOLVER POR METODO DE SUSTITUCION:

1. Se despeja una incógnita en una de las ecuaciones.

2. Se sustituye la expresión de esta incógnita en la otra ecuación, obteniendo un ecuación con una sola incógnita.

3. Se resuelve la ecuación.

4. El valor obtenido se sustituye en la ecuación en la que aparecía la incógnita despejada.

5. Los dos valores obtenidos constituyen la solución del sistema

Y A CONTINUACION UN VIDEO:

                       
    .